Parser Freeware - 2018 Version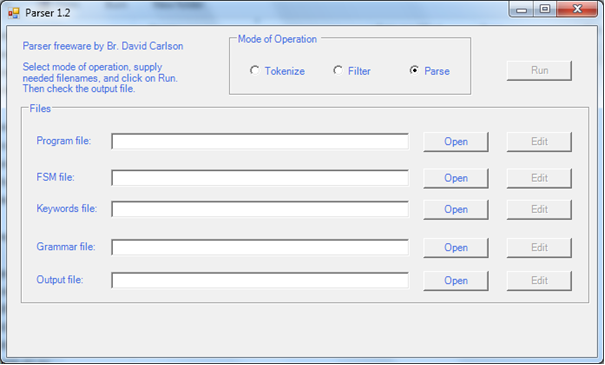
Parser for Educational UseThis freeware program provides an easy-to-use, table-driven LL(1) parser for educational use. The user supplies the program to be parsed as an input file, as well as files containing tables that specify the grammar rules, the finite state machine used to chop the program up into tokens, etc. The output, if parsing is successful, is an indented form of the parse tree for the given input program. The Parser can also be used to simply break the program up into a list of tokens, skipping the actual parsing. The .NET framework is needed in order to run this program. Available Items
Parsing Example 1This example illustates how to tokenize and parse programs consisting of blocks of simple assignment statements. Parsing Example 2This example adds the ability to parse IF...THEN...ELSE statements and FOR loops. Parsing Example 3This example adds more complicated arithmetic expressions. In the first two examples, an expression could only be a number or a variable. Now expressions can include ((x + 45) * num) and the like. The expressions are fully parenthesized. The reason that this is done is to enable us to tell the difference between an expression such as num + 1 and the simpler expression num. Both start with an identifier. With just one lookahead symbol, our LL(1) parser would not be able to tell which grammar rule to use on these with just the lookahead symbol num available. But when we require parentheses when doing arithmetic, the leading parenthesis tells us, and the parser, which grammar rule to use. See grammar rules 9 and 16 in the grammar file listed below. Note that in this example, the FSM file had to be changed to handle the ( and ) parentheses symbols as well as the -, *, and / arithmetic symbols. The first two take the finite state machine from state 1 to state 4. Any symbol that follows causes the finite state machine to recognize the ( or ) as a special token. Similarly, the -, *, / (or the + that was already in this machine) take the machine from state 1 to state 6, where any additional symbol other than an = causes the machine to recognize the -, *, /, or + as a special symbol. If the arithmetic operator is followed by an =, that takes the machine from state 6 to state 4, which enables the machine to recognize special tokens such as += and *=. Do you see how this finite state machine handles <, <=, >, and >= with this table? |
 |
||
Computing & Information Systems |
|

 Search CIS Site
Tutorials
Search CIS Site
Tutorials
|