Finding Definite Integrals Using Mathematica
Example 1
First, set up your function as in this example:
In[17]:=
![]()
Out[17]=
![]()
You can also set up a and b, or just fill in their values in the formulas that follow:
In[18]:=
![]()
Out[18]=
![]()
In[19]:=
![]()
Out[19]=
![]()
Our goal is to find the definite integral of f[x] from a to b. First we use the definition.
We begin with an appropriate Riemann sum. Here is a general way to write it:
In[20]:=
![]()
Out[20]=
![]()
In[21]:=
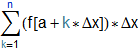
Out[21]=
![]()
Note that the sigma (sum) symbol can be found on the Basic Math Assistant palette (found under the Palettes menu).
Also note that the (b - a) / n is our Δx. The a + k * Δx steps through the right endpoints of our subintervals as k runs from 1 to n in the sum.
For example, when k = 1 we simply have a + Δx, the right endpoint of the first subinterval.
When k = 2 we get a + 2 * Δx, the right endpoint of the second subinterval.
When k = n we get a + n * Δx = a + n * (b - a) / n = a + (b - a) = b, which is the right endpoint of the last subinterval.
Finally, we take the limit of the Riemann sum. Just be sure it was the last item that you used shift-Enter on.
In[22]:=
![]()
Out[22]=
![]()
We can get a numeric value for the answer like this:
In[23]:=
![]()
Out[23]=
![]()
Let' s check our answer by using the numerical integration routine:
In[24]:=
![]()
Out[24]=
![]()
You can also use the Integrate function to try to get an exact answer. Sometimes this will fail, however.
In[25]:=
![]()
Out[25]=
![]()
In[26]:=
![]()
Out[26]=
![]()
You can also use the definite integral symbol from the Basic Math Assistant palette to try to get an exact answer. After placing it on the page, click on each little box. You can then type in the item that you want in that position.
In[27]:=
![]()
Out[27]=
![]()
In[28]:=
![]()
Out[28]=
![]()
Looks like we got it!
You can also use the Integrate function to try to get an exact answer. Sometimes this will fail, however.
Example 2
Let’s look at a different way to tell Mathematica to find a definite integral as the limit of a Riemann sum. For example, it might be easier to use h instead of Δx. Thus we start out as follows:
In[39]:=
![]()
Out[39]=
![]()
For an exponential function, make sure you use the number e on the Basic Math Assistant palette. Do NOT simply type an ordinary letter e. It will not work correctly.
In[40]:=
![]()
Out[40]=
![]()
In[41]:=
![]()
Out[41]=
![]()
In[42]:=
![]()
Out[42]=
![]()
It might also be easier to take the Limit of the Riemann sum directly, insead of doing the Riemann sum and then finding the limit of %, the last output:
In[43]:=
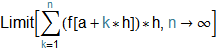
Out[43]=
![]()
![]()
Example 3
Here we try a harder exponential function.
In[44]:=
![]()
Out[44]=
![]()
Suppose that we want to integrate this function from 0 to 2. Let's try the definition first:
In[45]:=
![]()
Out[45]=
![]()
In[46]:=
![]()
Out[46]=
![]()
In[47]:=
![]()
Out[47]=
![]()
In[48]:=
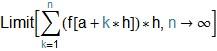
Out[48]=
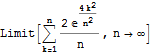
Note that Mathematica has refused to calculate the limit, or even the sum. It knows no method to do so.
We can try Integrate and NIntegrate:
In[49]:=
![]()
Out[49]=
![]()
This gave us an answer in terms of some other function. The problem is that f[x] has no closed-form antiderivative among
the elementary functions.
Perhaps we can get an approximate numerical result:
In[50]:=
![]()
Out[50]=
![]()
In[51]:=
![]()
Out[51]=
![]()
At least we succeeded in getting a numerical result.