![]()
![]()
![]()
In[1]:=
![]()
Out[1]=
![]()
![]()
In[2]:=
![]()
Out[2]=
![]()
![]()
In[3]:=
![]()
Out[3]=
![]()
![]()
![]()
In[4]:=
![]()
Out[4]=
![]()
In[5]:=
![]()
Out[5]=
![]()
![]()
In[7]:=
![]()
Out[7]=
![]()
![]()
In[8]:=
![]()
Out[8]=
![]()
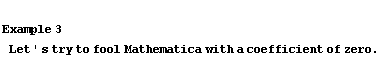
In[11]:=
![]()
Out[11]=
![]()
![]()
In[12]:=
![]()
Out[12]=
![]()
![]()
In[14]:=
![]()
Out[14]=
![]()
In[15]:=
![]()
Out[15]=
![]()
![]()
In[16]:=
![]()
Out[16]=
![]()
Created by Mathematica (January 31, 2004)